Refined oils
| Infobox on Refined oils | |
|---|---|
| Example of Refined oils |  |
| Facts | |
| Origin | - |
| Stowage factor (in m3/t) | 1,4 - 1,7 m3/t (drums) |
| Humidity / moisture | - |
| Ventilation | - |
| Risk factors | See text |
Refined oils
Description
An oil refinery or petroleum refinery is an industrial process plant where Crude Oil is processed and refined into more useful products such as petroleum naphtha, gasoline, diesel fuel, asphalt base, heating oil, kerosene, and liquefied petroleum gas. Oil refineries are typically large, sprawling industrial complexes with extensive piping running throughout, carrying streams of fluids between large chemical processing units. In many ways, oil refineries use much of the technology of, and can be thought of, as types of chemical plants. The crude oil feedstock has typically been processed by an oil production plant. There is usually an oil depot (tank farm) at or near an oil refinery for the storage of incoming crude oil feedstock as well as bulk liquid products.
An oil refinery is considered an essential part of the downstream side of the petroleum industry.
Raw or unprocessed crude oil is not generally useful in industrial applications, although "light, sweet" (low viscosity, low sulfur) crude oil has been used directly as a burner fuel to produce steam for the propulsion of seagoing vessels. The lighter elements, however, form explosive vapours in the fuel tanks and are therefore hazardous, especially in warships. Instead, the hundreds of different hydrocarbon molecules in crude oil are separated in a refinery into components which can be used as fuels, lubricants, and as feedstocks in petrochemical processes that manufacture such products as plastics, detergents, solvents, elastomers and fibres such as nylon and polyesters.
Petroleum fossil fuels are burned in internal combustion engines to provide power for ships, automobiles, aircraft engines, lawn mowers, chainsaws, and other machines. Different boiling points allow the hydrocarbons to be separated by distillation. Since the lighter liquid products are in great demand for use in internal combustion engines, a modern refinery will convert heavy hydrocarbons and lighter gaseous elements into these higher value products. The oil refinery in Haifa, Israel is capable of processing about 9 million tons (66 million barrels) of Crude Oil a year. Its two cooling towers are landmarks of the city's skyline.
Oil can be used in a variety of ways because it contains hydrocarbons of varying molecular masses, forms and lengths such as paraffins, aromatics, naphthenes (or cycloalkanes), alkenes, dienes, and alkynes. While the molecules in crude oil include different atoms such as sulfur and nitrogen, the hydrocarbons are the most common form of molecules, which are molecules of varying lengths and complexity made of hydrogen and carbon atoms, and a small number of oxygen atoms. The differences in the structure of these molecules account for their varying physical and chemical properties, and it is this variety that makes crude oil useful in a broad range of applications.
Once separated and purified of any contaminants and impurities, the fuel or lubricant can be sold without further processing. Smaller molecules such as isobutane and propylene or butylenes can be recombined to meet specific octane requirements by processes such as alkylation, or less commonly, dimerization. Octane grade of gasoline can also be improved by catalytic reforming, which involves removing hydrogen from hydrocarbons producing compounds with higher octane ratings such as aromatics. Intermediate products such as gasoils can even be reprocessed to break a heavy, long-chained oil into a lighter short-chained one, by various forms of cracking such as fluid catalytic cracking, thermal cracking, and hydrocracking. The final step in gasoline production is the blending of fuels with different octane ratings, vapour pressures, and other properties to meet product specifications.
Oil refineries are large scale plants, processing about a hundred thousand to several hundred thousand barrels of crude oil a day. Because of the high capacity, many of the units operate continuously, as opposed to processing in batches, at steady state or nearly steady state for months to years. The high capacity also makes process optimization and advanced process control very desirable.
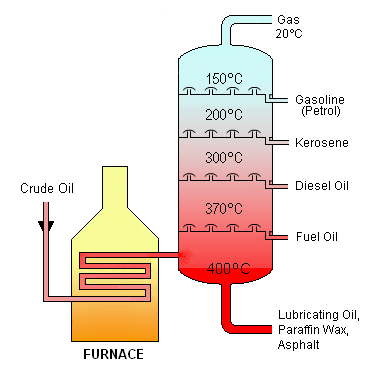
Petroleum products are usually grouped into three categories: light distillates (LPG, gasoline, naphtha), middle distillates (kerosene, diesel), heavy distillates and residuum (heavy fuel oil, Lubricating Oils, wax, asphalt). This classification is based on the way crude oil is distilled and separated into fractions (called distillates and residuum) as in the above drawing.
Application
- Liquified petroleum gas (LPG)
- Gasoline (also known as petrol)
- Naphtha
- Kerosene and related jet aircraft fuels
- Diesel fuel
- Fuel oils
- Lubricating Oils
- Paraffin Wax
- Asphalt and tar
- Petroleum coke
- Sulfur
Oil refineries also produce various intermediate products such as hydrogen, light hydrocarbons, reformate and pyrolysis gasoline. These are not usually transported but instead are blended or processed further on-site. Chemical plants are thus often adjacent to oil refineries. For example, light hydrocarbons are steam-cracked in an ethylene plant, and the produced ethylene is polymerized to produce polyethene.
Shipment / Storage / Risk factors
After contamination with foreign substances may be re-fined, and by virtue of the high value of these commodities this is usually an economic proposition.
Oil contaminated by water can usually be separated to a great extent in storage tanks by allowing the water to settle to the bottom and then draining off. It is impossible to effect clarification of the entire quantity, some residue will always remain.
Where oils are shipped in drums immediate steps should be taken to decant contents of leaky drums into sound drums.
See also Bulk Oils and Fats and Petroleum and Petroleum Products